ペントミノ 問題集
2つのL字型
問題1
まずはケースの中に入れる組み合わせのうち、図のように2つのL字形にしきられているものを作ってください。

長方形
ペントミノの駒はすべて正方形5個の集合体となっていますが、この正方形の一辺の単位を1とすると、ケースの大きさは6×10になります。しかし、このほかにもいろいろな形の長方形が作れます。
問題2
○3×20の長方形を作ってください(組み合わせ数は2通り)
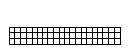
問題3
○4×15の長方形を作ってください(組み合わせ数は368通り)
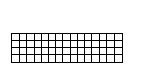
問題4
○5×12の長方形を作ってください(組み合わせ数は1,010通り)
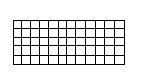
どれか1つの駒を拡大した形を作る
ケースからとり出して遊ぶ問題の中でも傑作といわれるものに、次のようなものがあります。12個の駒から3個をとりのぞき、残りの9駒で、とりのぞいた3個のうちのどれか1つの駒を拡大した形を作るものです。
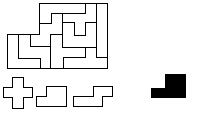
例:各辺が鍵の駒の3倍になる形を作る;鍵の駒
問題5
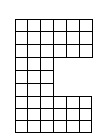
問題6
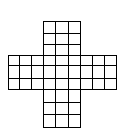
問題7

問題8
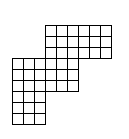
問題9
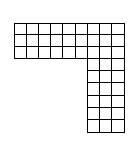
問題10
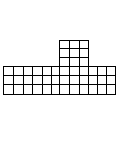
問題11
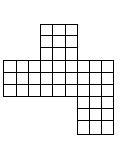
問題12
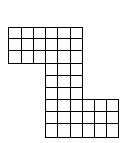
問題13
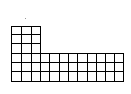
問題14
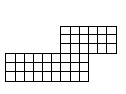
問題15
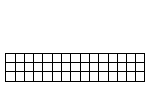
グループで同じ形を作る
問題16
12個の駒を6個ずつに分けたり、4個ずつに分けて、それぞれのグループで同じ形を作ることができます。図の形を作ってみてください。
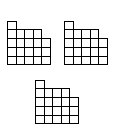
最大の長方形で最大の空間を作る
問題17
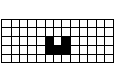
これは12個の駒で最大の長方形(8×11)を作りつつ、最大の長方形の空間(4×7)を作ったものです。

長方形に1×1の空間が3つ開ける
問題18
長方形の中央に駒の形の空間を作る
5×13の長方形を作りつつ、中央にそれぞれの駒の形の空間ができるようにします。

例
問題19
問題20
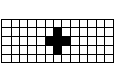
問題21

問題22
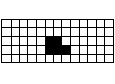
問題23
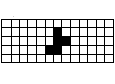
問題24
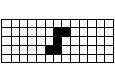
問題25
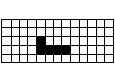
問題26
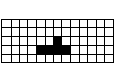
問題27
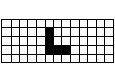
問題28

問題29

最後の問題
問題30
さて、いよいよ最後の問題です。おそらくこれはいちばんむずかしい問題となるでしょう。12個の駒をペントミノのケースに入れますが、全部の駒がケースのふちに接しているようにしてください。


